Finding posteriors through sampling
Bayesian data analysis is seen as a cutting-edge, up-and-coming method, even though Bayes’ Theorem dates back to 1763. Why is that? What stopped the Bayesian framework from taking off sooner?
The short answer: Computational limitations.
The slightly longer answer: Finding posterior distributions analytically (i.e., using calculus) works sometimes, but it’s not possible for every kind of model. Another way to find the posterior is to approximate it by drawing samples from it. This is computationally challenging, and it’s only fairly recently that sampling methods have been developed so that posteriors can be estimated by any old linguist with a laptop.
The method that brms uses is called Markov Chain Monte Carlo, or MCMC. It treats the posterior as a kind of landscape, and identifies the areas of highest probability essentially by running a physics simulation.
Imagine there’s a pit in the ground, and you throw a bouncy ball in. The ball will bounce around a lot, but most of the time, it’ll bounce toward/around the deepest point in the middle of the pit.
This means that, if every bounce is a sample, then you’ll have more samples from the part where the pit is deepest. If you take these samples and make a density plot, you’ll have higher density (because you have more samples) in the area of greatest depth.
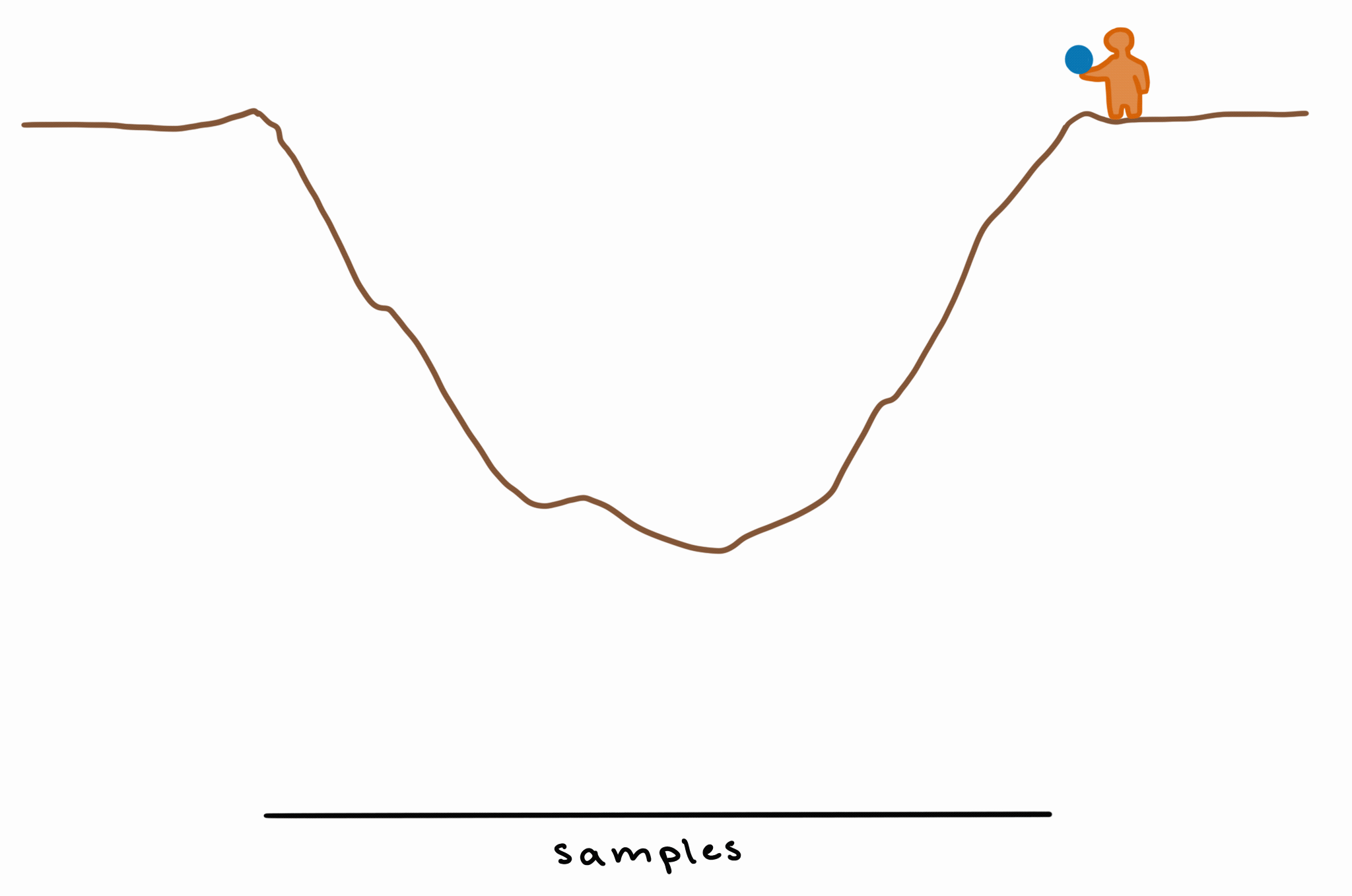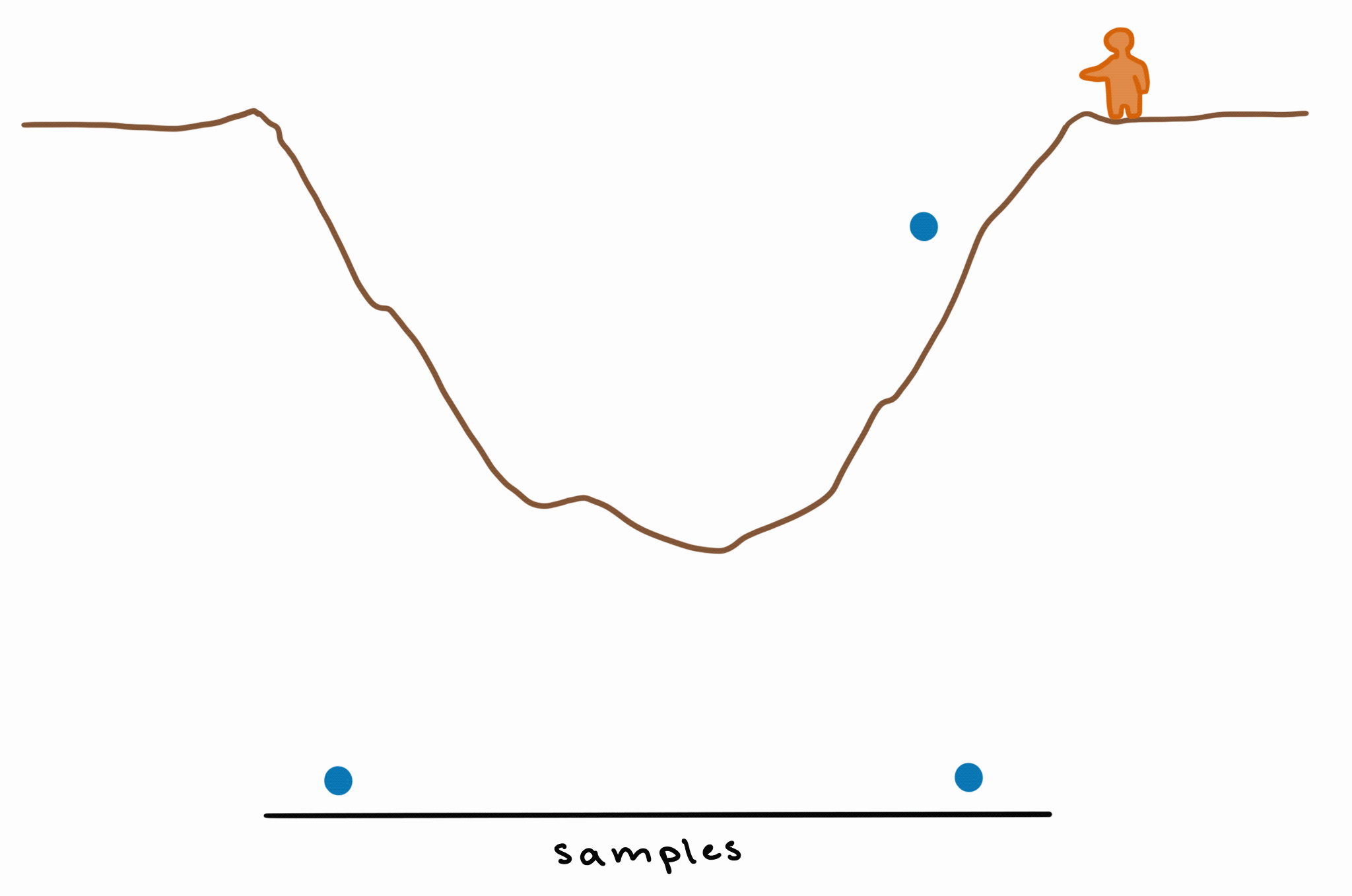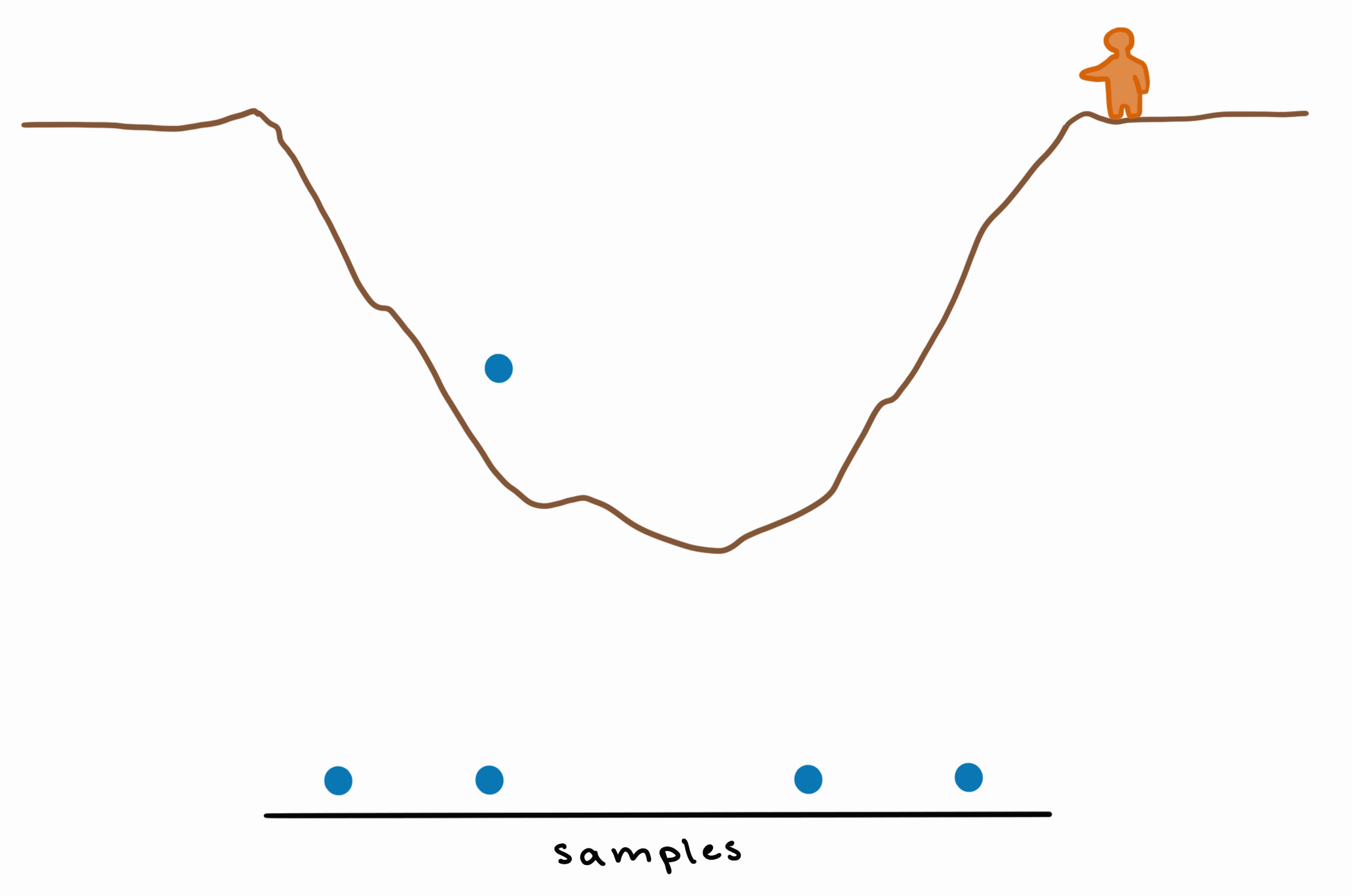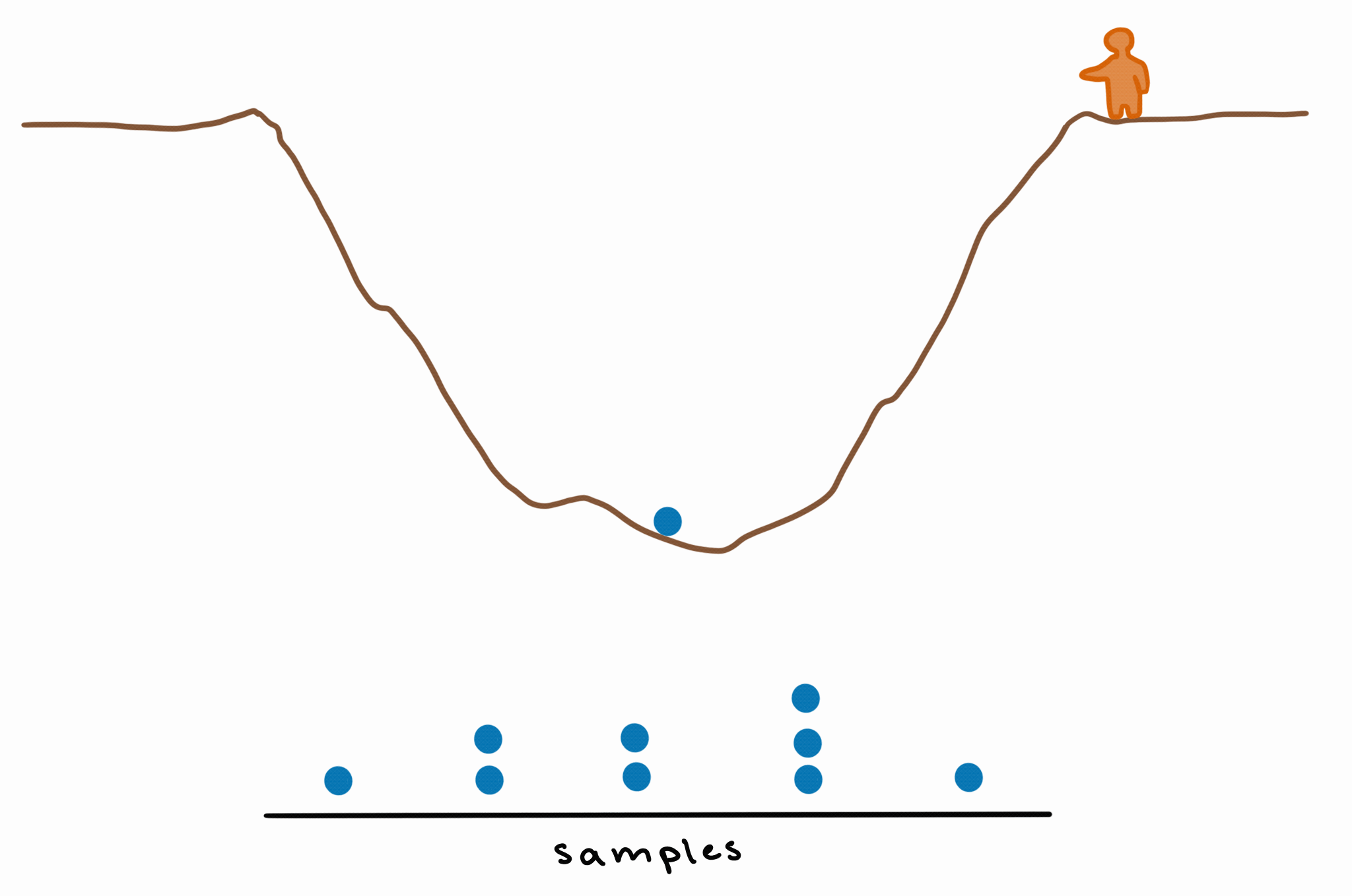
This is basically how MCMC works: by bouncing around the unknown/unknowable “landscape” of the posterior and exploring it by sampling, giving us more samples (= higher probability density) in those deeper (= higher-probability) areas.
If we take enough samples, we still get a decent approximation of the shape of the posterior, without needing to compute it exactly.
In reality, brms doesn’t just throw one proverbial bouncy ball into the proverbial pit, but four (and they’re also not called bouncy balls 😔 instead they’re called “chains”). These chains run, by default, for 2,000 iterations each.
- The first 1,000 iterations are used to explore the posterior landscape and hopefully eventually find a higher-probability area: this is called the “warm-up” or “burn-in” period.
- The next 1,000 iterations are spent traversing the posterior and drawing samples. And it’s those samples that brms will summarise when it describes each parameter’s posterior to us.